4 Sistema de tanque con una válvula de resistencia descrita por un gráfico
Problema 5.3 (Process Systems Analysis and Control - Coughanowr, LeBlanc)
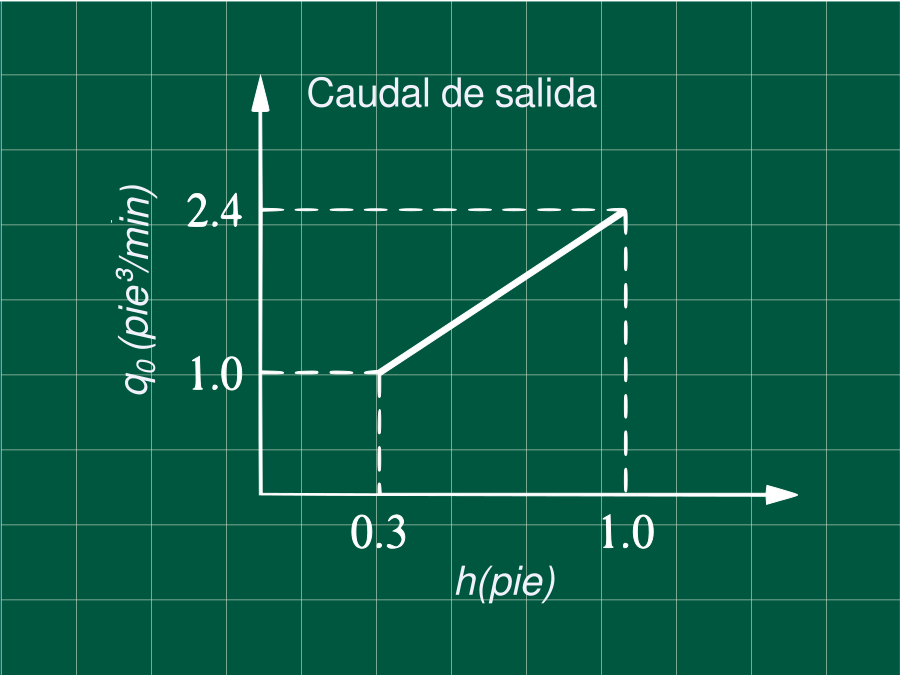
Un tanque con un área seccional de 2 pie² opera en estado estacionario con un flujo de entrada de 2 pie³/min. El flujo de salida vs la altura del sistema son representados en la figura.
Encuentre:
La función transferencia H(s)/Q(s).
Si el flujo hacia el tanque se incrementa en de 2.0 a 2.2 pie³/min (paso unitario), calcule el nivel h, 2 minutos después del cambio.
\begin{array}{l} Datos\\ A = 2\space pie²\\ q_s = 2\space pie³/min \end{array}
Obtención de la ecuación q_0
Como se observa en la gráfica q_0 es función de la altura y es una recta. Usando la fórmula de la ecuación de la recta que pasa por dos puntos tenemos (h_{1}=0.3,q_{01}=1) y (h_{2}=1,q_{02}=2.4) :
\frac{q_0-q_{01}}{h-h_1}=\frac{q_{02}-q_{01}}{h_2 - h_1}\\ \frac{q_0-1}{h-0.3}=\frac{2.4-1}{1 - 0.3}\\ q_0 = 2h+0.4
Escribiendo las ecuaciones de balance q - q_0 = \frac{dV}{dt}
Pero q_0 = 2h+0.4 y dV = Adh
q- (2h+0.4) = A\frac{dh}{dt} \space\space\space\space (1)
Escribiendo el balance en estado estacionario
q_s- (2h_s+0.4) = 0 \space\space\space\space (2)
Restando (1) con (2) para obtener las variables desviación y recordando que dh=d(h-h_s), por ser h_s constante.
q-q_s-2(h-h_s)+=A\frac{d(h-h_s)}{dt}
Q - 2\cdot H = A\frac{dH}{dt}
Aplicando la tranformada de Laplacey sabiendo que H(t=0)= h-h_s=h_s-h_s=0
Q(s) - 2H(s) = A(sH(s)-H(t=0))\\ Q(s) - 2H(s) = AsH(s)
Despejando
\mathbf{\frac{H(s)}{Q(s)}=\frac{1}{2 s+2}} \space\space\space\space (3) \\
Descripción de la perturbación
La perturbación sólo va a afectar el caudal de ingreso, esta puede ser representado por la variable desviación Q(t)
Q(t)=q-q_s= \begin{cases} 2.0-2.0 &\text{si } t < 0 \\ 2.2-2.0 \space\ pie³/min &\text{si } t>0\\ \end{cases}
Q(t)= \begin{cases} 0 &\text{si } t < 0 \\ 0.2 \space\ pie³/min &\text{si } t>0\\ \end{cases}
Expresando la misma función con impulsos unitarios y aplicando la transformada de Laplace
Q(t) = 0.2\cdot u(t) Entonces
Q(s) = \frac{0.2}{s}
Resolviendo para h(t=2)
Reemplazando la expresión anterior en la ecuación (3)
\begin{array}{l} H(s)= Q(s)\cdot \frac{1}{2s+2} \\ \\ H(s) = \frac{0.2}{s(2s+2)}\\ \end{array}
Operando para realizar la antitransformada
H(s) = \frac{0.2+0.2s-0.2s}{s(2s+2)}=\frac{0.1(2s+2)}{s(2s+2)}-\frac{0.2s}{s(2s+2)}
H(s) = \frac{0.1}{s}-\frac{0.1}{(s+1)}\\
Aplicando la antitransformada L^{-1}\{\space\}
Recuerde L^{-1}\{\frac{1}{s+k}\}= e^{-kt}
H(t) = 0.1-0.1\cdot e^{-t}
Calculando h(t=2)
De la ecuación en estado estacionario
q_s-(2h_s+0.4)=0 => h_s=0.8
Entonces
h(t=2) = H(t=2) + h_s
h(t=2)=0.1\cdot (1-e^{-2})+0.8
\mathbf{h(t=2)=0.8865\text{ pie}}
Referencias
- Coughanowr, D. R.; LeBlanc, S. E. (2009). Process Systems Analysis and Control (3rd edition). McGraw-Hill. ISBN 978-0-07-339789-4.