Resuelve tu sistema de EDO's con valores iniciales con RK4, Python y NumPy

Un poco acerca de NumPy

NumPy (Numerical Python), es unalibrería que da soporte para crear vectores y matrices en formato de numpy-arrays, lo cuál es un ventaja pues simplifica las operaciones entre ellas. (Es una librería que tiene mucho parecido con MatLab).

Para instalar numpy puedes hacerlo con conda, también puedes visitar si página web para ver otras opciones de instalación Numpy

1conda install numpy

Método de runge kutta 4° orden

El método de Runge Kutta 4°Orden, es una variación del método de Euler, el cuál permite resolver ecuaciones diferenciales ordinarias con condiciones iniciales. Vease Runge Kutta 4

La forma general de la variación del método de Euler es :

$$ y_{i+1} = y_i+\Phi h $$

$h$ representa el paso de integración, y $\Phi$ es la estimación de la pendiente o la derivada evaluada en $(x_i,y_i)$.

Para RK4 la ecuación completa sería:

$$ y_{i+1}=y_i+\frac{(k_1+2k_2+2k_3+k_4)}{6}h $$

Donde: $$ \begin{array}{l} k_1 = f(x_i,y_i) \ k_2 = f(x_i+h/2,y_i+k_1h/2) \ k_3 = f(x_i+h/2,y_i+k_2h/2) \ k_4 = f(x_i+h,y_i+k_3h) \end{array} $$

La función $f(x_i,y_i)$ es igual a $\frac{dy}{dx}$ evaluada en $(x_i,y_i)$.

Cambienos un poco la notación para dar a entender que usamos vectores.

$$ Z_{i+1}=Z_i+\frac{(M_1+2M_2+2M_3+M_4)}{6}h $$

$$ \begin{array}{l} M_1 = f(t_i,Z_i) \ M_2 = f(t_i+h/2,Z_i+m_1h/2) \ M_3 = f(t_i+h/2,Z_i+m_2h/2) \ M_4 = f(t_i+h,Z_i+m_3h) \end{array} $$

La codificación en python usando NumPy será muy similar a la notación vectorial que usamos arriba, la ventaja más importante trabajando con Numpy es el uso de sus vectores o matrices con el tipo de dato de numpy-arrays, estos nos permiten realizar operaciones entre ellas más fácilmente y al mismo tiempo tratarlas como si fueran listas de python.

Por ejemplo si tenemos un vector $A$ con componentes $(a_1,a_2,a_3)$ y $B$ con $(b_1,b_2,b_3)$ y queremos obtener un vector $C$ con componentes $(a_1/2+4b_1,a_2/2+4b_2,a_3/2+4b_3)$ esto se lo hace fácilmente con los numpy-array, simplemente haciendo las operación como si fueran valores numéricos:

$$ A = (a_1,a_2,a_3) \ B = (b_1,b_2,b_3) \ C = A/2+4*B $$

Con numpy array dando valores numéricos a los componenetes de los vectores $A$ y $B$.

1import numpy as np
2A = np.array([1, 2, 3])
3B = np.array([2, 4, 6])
4C = A / 2 + 4 * B
5
6print(C)
7# Resultado [ 8.5 17.  25.5]

Usted pude hacer las comprobaciones correspondientes con el código mostrado, si cada elemento de un vector numpy se le puede asignar los valores así de fácil, la codificación del método se simplifica bastante.

Normalmente en los sistemas de ecuaciones diferenciales no aparece la variable independente (tiempo $t$) por lo que las derivadas son independientes de la misma. En la codificiación se notará eso, se omitira la variable independiente $t$.

Codificando RK4

 1# archivo rk4.py
 2"""
 3Valores de entrada:
 4
 5sist_edo (function):    Contiene el sistema de ecuaciones diferenciales
 6                        retorna las derivadas evaluadas.
 7
 8rango_t (list):         Tiene la forma [t_ini, t_end] rango en cual
 9                        se va a resolver el sistema
10
11h(float):               (valor opcional) Paso de integración,
12                        por defecto 0.01
13
14Valores de Salida
15
16Z(np.array):            Matriz que contiene la solución del sistema,
17                        cada columna representa una variable y cada
18                        fila la variación de las variables de acuerdo
19                        a la variable independiente t
20"""
21
22import numpy as np
23
24
25def rungek4(sist_edo, rango_t, Z0, h=0.01):
26    t0, tf = rango_t
27    t = np.arange(t0, tf + h, h)
28    nt = len(t)
29    nz = len(Z0)
30    Z = np.zeros((nt, nz))
31    Z[0] = Z0
32
33    for i in range(1, nt):
34        M1 = sist_edo(Z[i - 1])
35        M2 = sist_edo(Z[i - 1] + h * M1 / 2)
36        M3 = sist_edo(Z[i - 1] + h * M2 / 2)
37        M4 = sist_edo(Z[i - 1] + h * M3)
38        Z[i] = Z[i - 1] + h * (M1 + 2 * M2 + 2 * M3 + M4) / 6
39
40    return Z
41    

Ahora que ya tenemos programado nuestro método podemos probarlo resolviendo un ejemplo

Resolución de un sistema de ecuaciones diferenciales

Conversión de Glucosa a Ácido glucónico

La conversión de glucosa a Ácido Glucónico es una simple oxidación del grupo aldehido del azucar a uno del grupo carboxilo. Esta transformación puede ser llevada a cabo por un microorganismo en un proceso de fermentación. La enzima Glucosa Oxidasa presente en el microorganismo, convierte la Glucosa a Gluconolactona. A su vez la gluconolactona se hidroliza a la forma de ácido glucónico. Todo el proceso de fermentación puede ser descrito como sigue:

Crecimiento celular $$ Glucosa + Células \Longrightarrow más\space Células $$

Oxidación de la glucosa por acción de la Glucosa Oxidasa $$ Glucosa + O_2 \Longrightarrow Gluconolactona + H_2O_2 $$

Hidrólisis de la Gluconolactona $$ Gluconolactona + H_2O \Longrightarrow Ácido Glucónico $$

Descomposición del Peroxido de Hidrógeno $$ H_2O_2\Longrightarrow H_2O+1/2O_2 $$

Un modelos matemático de la fermentación de la bacteria Pseudomonas Ovali, el cuál produce ácido glucónico, ha sido desarrolaldo pro Rai y Constatinides, este modelo, el cual describe la dinámica en la fase logaritmica, puede ser descrito como sigue:

Velocidad de crecimiento celular $$ \frac{dy_1}{dt} =b_1y_1 \left(1-\frac{y_1}{b_2} \right) $$

Velocidad de formación de gluconolactona $$ \frac{dy_2}{dt}=\frac{b_3y_1y_4}{b_4+y_4}-0.9082b_5y_2 $$

Velocidad de formación de ácido glucónico $$ \frac{dy_3}{dt}=b_5y_2 $$

Velocidad de consumo de glucosa $$ \frac{dy_4}{dt}=-1.011 \left(\frac{b_3y_1y_4}{b_4+y_4}\right) $$

Donde: $y_1$: Concentración de células. $y_2$: Concentración de Gluconolactona. $y_3$: Concentración de Ácido glucónico. $y_4$: Concentración de Glucosa. $b_1-b_5$: Parámetros que son función de la temperatura y el pH.

Las condicionas de operaciónson 30°C y el pH 6.6, para los cuales los parámetros son: $b_1=0.949$; $\space\space b_2=3.439$; $\space\space b_3=18.72$; $\space\space b_4=37.51$; $\space\space b_5= 1.169$.

Con los datos proporcionados halle las concentraciones en el rango de 0h a 10h. Si las condiciones iniciales son:

$y_1(0) = 0.5 \space U.O.D./mL$; $\space\space y_2(0)=0.0mg/mL$: $\space\space y_3(0)=0.0 mg/mL$; $\space\space y_4(0)=50.0 mg/mL$

 1# archivo solver_EDO.py
 2import rk4
 3import numpy as np
 4import matplotlib.pyplot as plt
 5
 6
 7"""
 8Función que define el sistema de ecuaciones diferenciales de la 
 9conversión del a glucosa a Ácido Glucónico
10
11Entrada:
12Y(lista, np-array):     Vector que contiene las variables que van a servir 
13                        para evaluar la derivada.
14
15Salida:
16dy(lista, np-array):    Vector que contiene las derivadas.
17"""
18
19
20def glucosa2ac_gluconico(Y):
21    dy = np.zeros(len(Y))
22    b1 = 0.949
23    b2 = 3.439
24    b3 = 18.72
25    b4 = 37.51
26    b5 = 1.169
27
28    dy[0] = b1*Y[0]*(1-Y[0]/b2)
29    dy[1] = b3*Y[0]*Y[3]/(b4+Y[3])-0.908*b5*Y[1]
30    dy[2] = b5*Y[1]
31    dy[3] = -1.011*b3*Y[0]*Y[3]/(b4+Y[3])
32
33    return dy
34
35
36# Resolvemos el sistema de ecuaciones diferenciales con rk4
37# Aunque las unidades de las constantes no nos la dan, podemos azumir que son 
38# compatibles con las unidades de tiempo en horas
39rango_t = [0, 10]
40h = 0.01
41t = np.arange(rango_t[0], rango_t[1] + h, h)
42# Definimos las condiciones iniciales
43Y0 = np.array([0.5, 0, 0, 50])
44Y = rk4.rungek4(glucosa2ac_gluconico, rango_t, Y0, h)
45
46# Graficando la solución
47
48font = {'family': 'serif',
49        'color': 'xkcd:black',
50        'weight': 'normal',
51        'size': 12,
52        }
53    
54plt.plot(t, Y[:, 0], label="Células")
55plt.plot(t, Y[:, 1], label="Gluconolactona")
56plt.plot(t, Y[:, 2], label="Ácido Glucónico")
57plt.plot(t, Y[:, 3], label="Glucosa")
58plt.legend(loc=5)
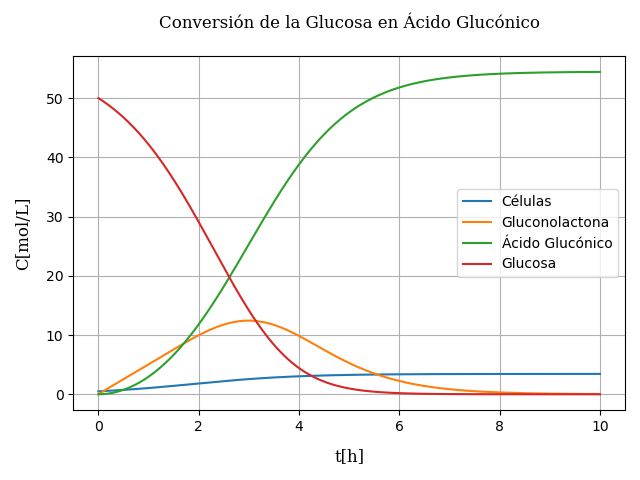
59plt.title("Conversión de la Glucosa en Ácido Glucónico", fontdict=font, pad=20)
60plt.xlabel("t[h]", labelpad=10, fontdict=font)
61plt.ylabel("C[mol/L]", labelpad=10, fontdict=font)
62plt.grid()
63plt.show()

La gráfica solución es: