Problema secado

Problema secado

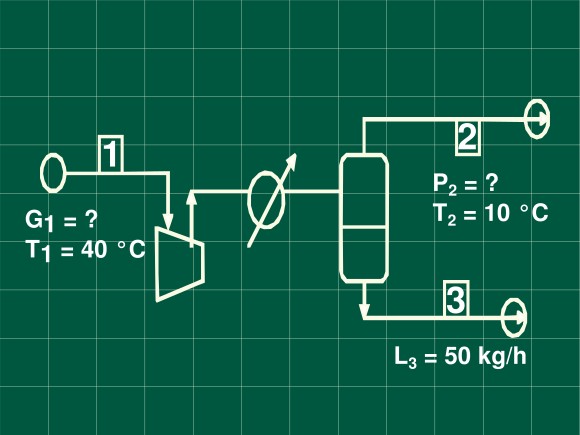
En una mezcla de benceno y nitrógeno, que está a 40 °C y 720 mm de Hg, la presión parcial del benceno es de 50 mm de Hg. Para separar el 80 % del benceno presente, la mezcla se somete a enfriamiento y compresión. Calcule:

• a) La presión final si se enfría hasta 10 º C
• b) El volumen inicial de la mezcla para condensar 50 kg / h de benceno

Consideraciones

Como hay condensación la masa gaseosa quedará saturada a la temperatura final de enfriamiento.

Balance de masa

Total

$$ G_{1} = L_{3} + G_{2} $$

Parcial de benceno

$$ G_{1}y_{1} = L_{3}x_{3} + G_{2}y_{2} $$

Ecuaciones para operaciones de vapores con gases

$$ Y_{1} = \frac{y_{1}}{1 - y_{1}} $$

$$ G_{S} = G_{1}(1 - y_{1}) $$

$$ \frac{G_{S}}{(1 - y_{1})}y_{1} = L_{3}x_{3} + \frac{G_{S}}{(1 - y_{2})}y_{2} $$

$$ G_{S}Y_{1} = L_{3}x_{3} + G_{S}Y_{2} $$

$$ L_{3} = G_{S}(Y_{1} - Y_{2}) $$

$$ G_{1} = G_{S}V_{H} $$

Cálculos

Humedad inicial

$$ Y_{1} = \frac{50}{720 - 50} \cdot \frac{78}{28} = 0.208\ \frac{\text{kg\ benceno}}{kg\ nitrógeno} $$

Humedad final

Como se condensa el 80 % del benceno entrante

$$ Y_{2} = 0.208\left( 0.2 \right) = 0.0416\ \frac{\text{kg\ benceno}}{kg\ nitrógeno} $$

Presión de vapor de benceno a 10ºC Constantes de Antoine A = 7.429; B = 1628.32; C = 279.56

$$ \log{P{^\circ}} = 7.429 - \ \frac{1628.32}{10 + 279.56} = 1.8055 $$

$$ P{^\circ} = 63.9\ mmHg $$

Presión final $$ Y_{2} = 0.0416 = \frac{63.91}{P_{T} - 63.91} \bullet \frac{78}{28} $$

Benceno condensado por kilogramo de nitrógeno

$$ \mathrm{\Delta}Y = 0.208 - 0.0416 = 0.1664\frac{\text{kg\ benceno}}{kg\ nitrógeno} $$

Volumen húmedo de la corriente

$$ V_{H} = \left( \frac{1}{28} + \frac{0.208}{78} \right)\frac{0.082*313}{\frac{720}{760}} = 1.04\frac{m^{3}}{\text{kg\ }N_{2}} $$

Volumen inicial

$$ V = \frac{50\ kg\ de\frac{\text{benceno}}{h}}{0.1664\frac{\text{kg\ benceno}}{\text{kg\ }N_{2}}}\left( 1.04\frac{m^{3}}{\text{kg\ }N_{2}} \right) = 312.5\frac{m^{3}\text{\ de\ mezcla}}{h} $$

Resultados

La presión final es de 5.716 atm. Se requieren $312.5 m^{3}/h$ de mezcla para condensar $50 kg / h$.