Método gráfico Mc-Cabe Thiele para destilación binaria, implementado con python
Introducción
El método gráfico de McCabe Thiele es usado para calcular el número de etapas en una destilación binaria, este método asume que:
- La columna de destilación es adiabática.
- Por cada mol de vapor condensado hay un mol de liquido que se evapora.
- La variación del calor sensible es despreciable en comparación de calor latente.
- El calor de vaporización es el mismo para ambos componentes, independientemente de la concentración.
- El calor de mezcla es despreciable.
Para el primer ejemplo se utilizara datos experimentales de la curva de equilibrio y-x, siendo x, y las fracciones molares del componente más volátil.
Las ecuaciones que gobiernan el método de MCCabe Thiele son:
Línea de rectificación
$$ y_{R} = \frac{R}{R+1}x+\frac{1}{R+1}x_D $$
Con $R=L/D$ que es el fracción de reflujo.
Línea de Alimentación
$$ y_F = \frac{q}{q-1}x-\frac{1}{q-1}x_F $$
Donde $q=\frac{H_V-H_F}{H_V-H_L}$ que es la calidad de vapor de la alimentación.
Línea de Agotamiento
$$ y_{S}=\frac{L}{V}x+\frac{W}{V}x_W $$
La línea de agotamiento ($y_S$), también puede obtener vía las siguientes ecuaciones:
Obtenemos la intersección de las línea de rectificación y de alimentación $(x_{int},y_{int})$ $$ x_{int}= \frac{x_D(q-1)+z_F(R+1)}{q+R} $$
$$ y_{int}=y_F(x_{int})=y_R(x{int}) $$
Con el punto de intersección $(x_{int},y_{int})$ y $x_W$, podemos contruir la línea de agotamiento
$$ y_S = \frac{y_{int}-x_W}{x_int-x_W}(x-x_W)+x_W $$
Cálculo del reflujo mínimo
El reflujo mínimo puede ser calculado como sigue:
$$ \frac{x_D-y^*}{x_D-x^*}=\frac{R_{min}}{R_{min}+1}=\frac{1}{k} $$
$$ R_{min}= \frac{1}{k-1} $$
Ejemplo
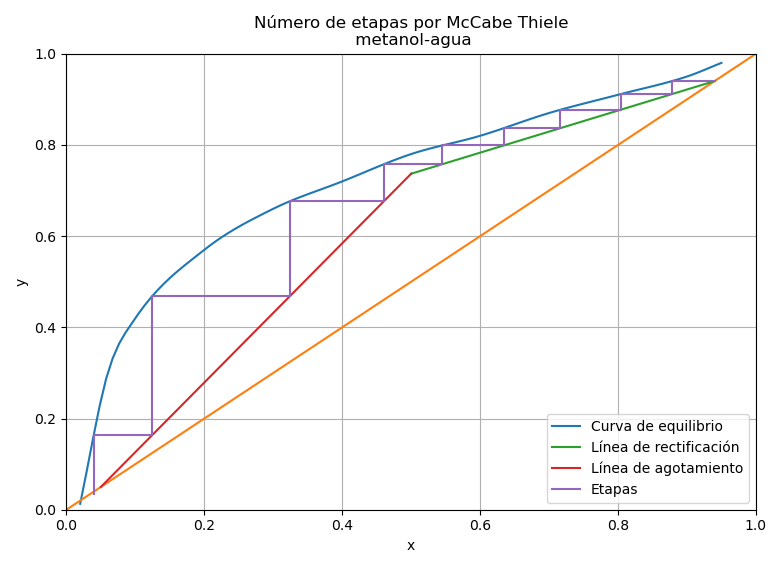
Se requiere alimentar una columna de destilación una corriente de agua y metanol a un flujo de 1000 mol/h con 0.5 de fracción molar de metanol en su punto de burbuja, estime el número de etapas requeridas si se quiere obtener un destilado de 0.94 en fracción molar de metanol y un condensado al 0.05 en fracción molar de metanol. use el método de McCabe Thiele para la estimación del número de etapas,considetando el el reflujo es igual a 1.5 veces el reflujo mínimo.
Considere los siguientes datos como la curva de equilibrio y-x.
$$ \begin{array}{c|c} x & y \\ \hline 0.02 & 0.013 \\ \hline 0.06 & 0.3 \\ \hline 0.1 & 0.42 \\ \hline 0.2 & 0.57 \\ \hline 0.3 & 0.66 \\ \hline 0.4 & 0.72 \\ \hline 0.5 & 0.78 \\ \hline 0.6 & 0.82 \\ \hline 0.7 & 0.87 \\ \hline 0.8 & 0.91 \\ \hline 0.9 & 0.95 \\ \hline 0.95 & 0.98 \\ \hline \end{array} $$
Para resolver el ejercicio vamos necesitar de interpolar muchas veces la curva de equilibrio, por lo que vamos interpolarla de una serie de datos interpolados con el método de interpolación cúbica monotónica de Hermite.
1
2import math
3import numpy as np
4
5
6def h00(t):
7 return 2*t**3-3*t**2+1
8
9
10def h10(t):
11 return t**3-2*t**2+t
12
13
14def h01(t):
15 return -2*t**3+3*t**2
16
17
18def h11(t):
19 return t**3-t**2
20
21
22def pchint(x, y, x0):
23 n = len(x)
24 d = np.zeros(n-1)
25 for i in range(n-1):
26 d[i] = (y[i+1]-y[i])/(x[i+1]-x[i])
27
28 m = np.zeros(n)
29 m[0] = d[0]
30 m[-1] = d[-1]
31
32 for i in range(1, n-1):
33 if d[i-1]*d[i] < 0:
34 m[i] = 0
35 else:
36 m[i] = (d[i-1]+d[i])/2
37
38 for i in range(n-1):
39 if y[i] == y[i+1]:
40 m[i] = 0
41 m[i+1] = 0
42
43 for i in range(n-1):
44 if m[i] != 0:
45 alfa = m[i]/d[i]
46 beta = m[i+1]/d[i]
47
48 condicion = alfa - ((2*alfa+beta-3)**2)/(alfa+beta-2)/3
49
50 while condicion < 0:
51 tau = 3/math.sqrt(alfa**2+beta**2)
52 alfa = tau*alfa
53 beta = tau*beta
54 m[i] = alfa*d[i]
55 m[i+1] = beta*d[i]
56 condicion = alfa - ((2*alfa+beta-3)**2)/(alfa+beta-2)/3
57 pos = 0
58 c = 0
59 F = np.zeros(len(x0))
60
61 for xi in x0:
62 if xi > x[pos+1]:
63 pos += 1
64
65 delta = x[pos+1]-x[pos]
66 t = (xi-x[pos])/delta
67 F[c] = y[pos]*h00(t)+delta*m[pos]*h10(t)+y[pos+1]*h01(t)+delta*m[pos+1]*h11(t)
68 c += 1
69 return F
Con el algoritmo de interpolación definido podemos codificar en python. Puede descargar los datos de equilibrio aquí, guardelo con el nombre de agua-metanol.csv
1
2from hermite import pchint
3import numpy as np
4import matplotlib.pyplot as plt
5import csv
6
7
8def open_data(location):
9 x, y = [], []
10
11 with open(location, "r") as f:
12 reader = csv.DictReader(f)
13 for row in reader:
14 x.append(float(row["x"]))
15 y.append(float(row["y"]))
16 return x, y
17
18
19def eq_line(a, b):
20 return lambda x: a + b * x
21
22# Obteniendo la curva interpolada
23
24
25def inter_vline(x, data_x, data_y):
26 n = len(data_x)
27 i, j = 0, n - 1
28 while (j - i) >= 2:
29 m = (j + i) // 2
30 if data_x[m] > x:
31 j = m
32 else:
33 i = m
34 slope = (data_y[j] - data_y[i]) / (data_x[j] - data_x[i])
35 origin = -slope * data_x[i] + data_y[i]
36 line2 = eq_line(origin, slope)
37 return x, line2(x)
38
39
40def inter_line(line, data_x, data_y):
41 n = len(data_x)
42 i, j = 0, n - 1
43
44 while (j - i) >= 2:
45 m = (j + i) // 2
46 if (data_y[m] - line(data_x[m])) * (data_y[j] - line(data_x[j])) < 0:
47 i = m
48 else:
49 j = m
50
51 slope = (data_y[j] - data_y[i]) / (data_x[j] - data_x[i])
52 origin = -slope * data_x[i] + data_y[i]
53 line2 = eq_line(origin, slope)
54 f1 = line2(0) - line(0)
55 f2 = line2(1) - line(1)
56 x_in = f1 / (f1 - f2)
57 y_in = line(x_in)
58
59 return x_in, y_in
60
61
62def reflux_min(x_in, y_in, x_D):
63 k = (x_D - x_in) / (x_D - y_in)
64 R = 1 / (k - 1)
65 return R
66
67
68def solve_mccabe_thiele():
69 data_x, data_y = open_data("agua-metanol.csv")
70 # obtención de datos interpolados
71 x0 = np.linspace(data_x[0], data_x[-1], 100)
72 y0 = pchint(data_x, data_y, x0)
73
74 xF = 0.5
75 xD = 0.94
76 xW = 0.05
77
78 x_int, y_int = inter_vline(xF, x0, y0)
79 r_min = reflux_min(x_int, y_int, xD)
80 r = 1.5*r_min
81
82 line_recti = eq_line(xD/(r+1), r/(r+1))
83 yF = line_recti(xF)
84 slope = (xW - yF) / (xW - xF)
85 origin = -slope * xF + yF
86 line_strip = eq_line(origin, slope)
87
88 xe = []
89 ye = []
90 xp = xD
91 xe.append(xD)
92 ye.append(xD)
93 etapas = 0
94 while xp > xW:
95
96 line_xpn = eq_line(xp, 0)
97 xpn, xp = inter_line(line_xpn, x0, y0)
98
99 etapas += 1
100 ye.append(xp)
101 xe.append(xpn)
102
103 if xpn > xF:
104 xp = line_recti(xpn)
105 else:
106 xp = line_strip(xpn)
107
108 ye.append(xp)
109 xe.append(xpn)
110
111 print("etapas", etapas)
112 x_rect = np.linspace(xF, xD, 50)
113 y_rect = np.array([line_recti(x) for x in x_rect])
114 fig, ax = plt.subplots()
115 x_strip = np.linspace(xW, xF, 50)
116 y_strip = np.array([line_strip(c) for c in x_strip])
117
118 ax.plot(x0, y0, label="Curva de equilibrio")
119 ax.plot([0, 1], [0, 1])
120 ax.plot(x_rect, y_rect, label="Línea de rectificación")
121 ax.plot(x_strip, y_strip, label="Línea de agotamiento")
122 ax.plot(xe, ye, label="Etapas")
123 ax.set_title("Número de etapas por McCabe Thiele\n metanol-agua")
124 ax.set_ylabel("y")
125 ax.set_xlabel("x")
126 ax.set_xlim([0, 1])
127 ax.set_ylim([0, 1])
128 ax.grid()
129 plt.legend(loc="lower right")
130 plt.show()
131
132
133solve_mccabe_thiele()
Ejecutando la gráfica resultante sería:
Referencias
McCabe, W. L.; Smith, J. C. (1976). Unit Operations of Chemical Engineering (3rd edición). McGraw-Hill. ISBN 0-07-044825-6.
Fritsch & Carlson (1980), Monotone Piecewise Cubic Interpolation, doi:10.1137/0717021.