FLujo de gas en un destilador multicomponente

Problema

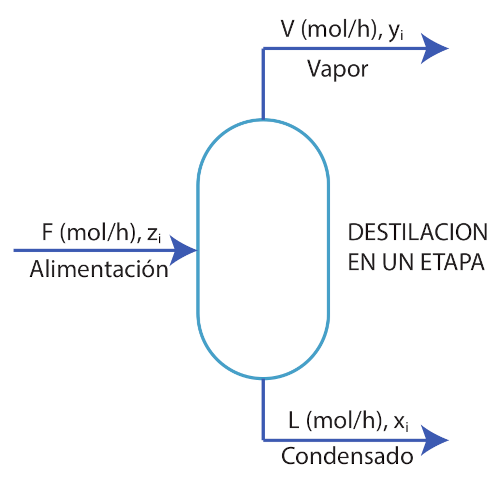
Usando los datos de la tabla de composiciones para un gas natural a $P = 11\space MPa\space$ y $\space T = 48 °C$. Resuelva para el flujo $V(mol/h)$ usando las ecuaciones de equilibrio, sabiendo que se tiene flujo molar de entrada $F = 100 mol/h$.

$$\begin{array}{c|c|c|c} Componente & i & z_{i} & k_{i} & \\\hline metano & 1 & 0.8345 & 3.090 &\\dioxido de carbono & 2 & 0.0046 & 1.650 &\\etano & 3 & 0.0381 & 0.720 &\\propano & 4 & 0.0163 & 0.390 &\\i-butano & 5 & 0.0050 & 0.210 &\\n-butano & 6 & 0.0074 & 0.175 &\\pentanos & 7 & 0.0287 & 0.093 &\\hexanos & 8 & 0.0220 & 0.065 &\\heptanos + & 9 & 0.0050 & 0.210 &\\\end{array}$$

Fuente: Geankoplis, C. J. (1993) Transport Processes and Unit Operations

Planteando las ecuaciones del balance másico:

$$\begin{array}{l} F&=, L + V \\z_{i}F &=, x_{i}L + y_{i}V \end{array}$$

Condiciones de equilibrio: $\space\space y_{i}=k_{i}x_{i}\space\space$; $\space\space\space\sum x_{i}=\sum y_{i}=1$

Combinando estas ecuaciones podemos obtener:

$$\sum_{i=1}^{n} \frac {z_{i}F}{V(k_{i}-1)+F}=1$$

Reordenando nuestra ecuación igualandola a cero:

$$foo(V)=\sum_{i=1}^{n} \frac {z_{i}F}{V(k_{i}-1)+F}-1=0$$

Nótese que para el valor correcto de $V$ nuestra función $foo(V)=0$

 1# Definimos la función foo
 2def foo(V):
 3    F = 100
 4    z = [
 5        0.8345,
 6        0.0046,
 7        0.0381,
 8        0.0163,
 9        0.0050,
10        0.0074,
11        0.0287,
12        0.0220,
13        0.0434
14    ]
15
16    k = [3.090,
17         1.650,
18         0.720,
19         0.390,
20         0.210,
21         0.175,
22         0.093,
23         0.065,
24         0.036
25         ]
26
27    n = len(z)
28    f = sum([z[i] * F / (V * (k[i] - 1) + F) for i in range(n)])
29    return f - 1
30
31
32# Definimos la función que va resolver el problema
33def equilibrio_LV():
34    a, b = 100, 80
35    c = b - foo(b) * (b - a) / (foo(b) - foo(a))
36    while abs(foo(c)) > 1e-4:
37        a, b = b, c
38        c = b - foo(b) * (b - a) / (foo(b) - foo(a))
39    return c
40
41
42print(equilibrio_LV())
43# Resultado 88.66942481438184

Nuestro resultado es $88.6694 \space mol/h$