Un sistema con un tanque, una bomba y una válvula

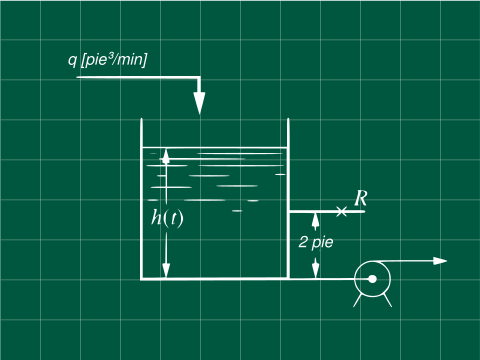
authorEver Vino calendarOct 6, 2022 · 2 min read · post control_automatico  ·
Compartir en: linkedincopy

Problema 5.1 (Process Systems Analysis and Control - Coughanowr, LeBlanc)

Derive la ecuación transferencia H(s)/Q(s) para el nivel del líquido del sistema mostrado en la figura, cuando el tanque opera en estado estacionario a:

  • a) $\text{ }h_s = 1 \text{ pie}$

  • b) $\text{ }h_s = 3 \text{ pie}$

La bomba extrae agua a caudal constante de $10\text{ pie³/min}$ y es independiente del la altura $h$, El área seccional es $A = 1.0\text{ pie²}$ y la resistencia es $R=0.5\text{ pie³/min}$.

Resolviendo para $h_s=1\text{pie}$

Cuando la altura $h_s=1$ podemos notar que no existe flujo posible por la válvula, por lo que no lo consideramos en la ecuación transferencia.

Escribiendo las ecuaciones de balance

$$ q - q_b = \frac{dV}{dt} = A\frac{dh}{dt} \space\space\space\space\space \textbf{(1)} $$

Ecuacion en estado estacionario

$$ q_s - q_b = 0 \space\space\space\space\space \textbf{(2)} $$

Restando (1) con (2) para obtener las variables desviación y recordando que $dh=d(h-h_s)$, por ser $h_s$ constante.

$$ q-q_s=A\frac{d(h-h_s)}{dt} $$

$$ Q = A\frac{dH}{dt} $$

Aplicando la tranformada de Laplace, sabiendo que $H(t=0)= h-h_s=h_s-h_s=0$ y $A=1\text{ pie}$.

$$ Q(s) = A(sH(s)-H(t=0))\ $$ $$ \mathbf{\frac{H(s)}{Q(s)} = \frac{1}{s}} $$

Resolviendo para $h_s=3\text{ pie}$

Cuando $h_s=3$ el sistema se encuentra operando sobre el nivel de la válvula, por lo que si existe un flujo $q_0$ que pasa por este.

Aplicando un balance del sistema y sabiendo que $q_0 = h-h_v/R$, donde $h_v$ es la altura de la válvula

$$ q - q_0- q_b = A\frac{dh}{dt} $$ $$ q - \frac{h-h_v}{R}- q_b = A\frac{dh}{dt} \space\space\space\space\space \textbf{(3)} $$

Balance en estado estacionario

$$ q_s - \frac{h_s-h_v}{R}- q_b = 0 \space\space\space\space\space \textbf{(4)} $$

Restando (3) con (4) para obtener las variables desviación y recordando que $dh=d(h-h_s)$, por ser $h_s$ constante.

$$ q - q_s- \frac{h-h_s}{R} = A\frac{d(h-h_s)}{dt} $$

$$ Q -\frac{H}{R} = A\frac{dH}{dt} $$

Aplicando la tranformada de Laplace, sabiendo que $H(t=0)= h-h_s=h_s-h_s=0$, $A=1\text{ pie}$ y $R=0.5\text{ pie/(pie³/min)}$.

$$ Q(s) -\frac{H(s)}{R} = A(sH(s)-H(t=0))\ $$ $$ \frac{H(s)}{Q(s)} = \frac{R}{ARs+1} $$

$$ \mathbf{\frac{H(s)}{Q(s)} = \frac{0.5}{0.5s+1}} $$

Referencias

  • Coughanowr, D. R.; LeBlanc, S. E. (2009). Process Systems Analysis and Control (3rd edition). McGraw-Hill. ISBN 978-0-07-339789-4.

Contenido